
On the first call, its value is initialValue if the latter is specified otherwise its value is array. The value resulting from the previous call to callbackFn. The function is called with the following arguments: accumulator For the last invocation, the return value becomes the return value of reduce(). Its return value becomes the value of the accumulator parameter on the next invocation of callbackFn. ()Ī function to execute for each element in the array.Object.prototype._lookupSetter_() Deprecated.Object.prototype._lookupGetter_() Deprecated.Object.prototype._defineSetter_() Deprecated.Object.prototype._defineGetter_() Deprecated.Since, we cannot have the logarithm of a negative number, then x = 2 remains to be the correct answer. Since argument of a logarithm cannot be negative, then the correct answer is x = 6. = log 3 (9) + log 3 (3) + 2log 3 x + 5log 3 yįind the value of x given, 2log x = 4log3Īpply the distributive property to remove brackets. This is a subtraction expression therefore, we apply the quotient rule law. Rewrite 32 in exponential form to get the value of its exponent. Given that, x = log aM then a log a M = a.The logarithm of any positive number to the same base is equal to 1.The logarithm of 1 to any finite non-zero base is zero.The logarithmic value of a negative number is imaginary.Natural logarithms are expressed as ln x, which is the same as log e The constant e is approximated as 2.7183. Logarithm to the base ‘e’ is called natural logarithms.When a logarithm is written without a subscript base, we assume the base to be 10. Logarithms to the base of 10 are referred to as common logarithms.Logarithmic values of a given number are different for different bases.The logarithm of a positive real number can be negative, zero or positive.Given that a n= b ⇔ log a b = n, the logarithm of the number b is only defined for positive real numbers.They are always applied under certain rules and regulations.įollowing rules needed to be remembered while playing with logarithms: Logarithms are a very disciplined field of mathematics. log 2 4x – log 2 x = log 2 (4x/x) = log 2 4.

Subtraction of two logarithms A and B is equal to dividing the logarithms. log 4x + log x = log (4x * x) = log 4x 2.The first law of logarithms state that the sum of two logarithms is equal to the product of the logarithms. The four basic laws of logarithms include: These laws can be applied on any base, but during a calculation, the same base is used. The logarithmic expressions can be written in different ways but under certain laws called laws of logarithms. Changing logarithmic functions to exponential form.We can use laws and rules of logarithms to perform the following operations: However, the same base must be used throughout a calculation. It is important to note that the laws and rules of logarithms apply to logarithms of any base. Like exponents, logarithms have rules and laws that work the same way as the rules of exponents. In calculus, the logarithm is used to differentiate complex problems and determine the area under curves.A logarithm is used to calculate the payment period of a loan.

Exponential processes such as the decay of ratio active isotopes, growth of bacteria, the spread of an epidemic in a population, and cooling of a dead body are analyzed using logarithms.
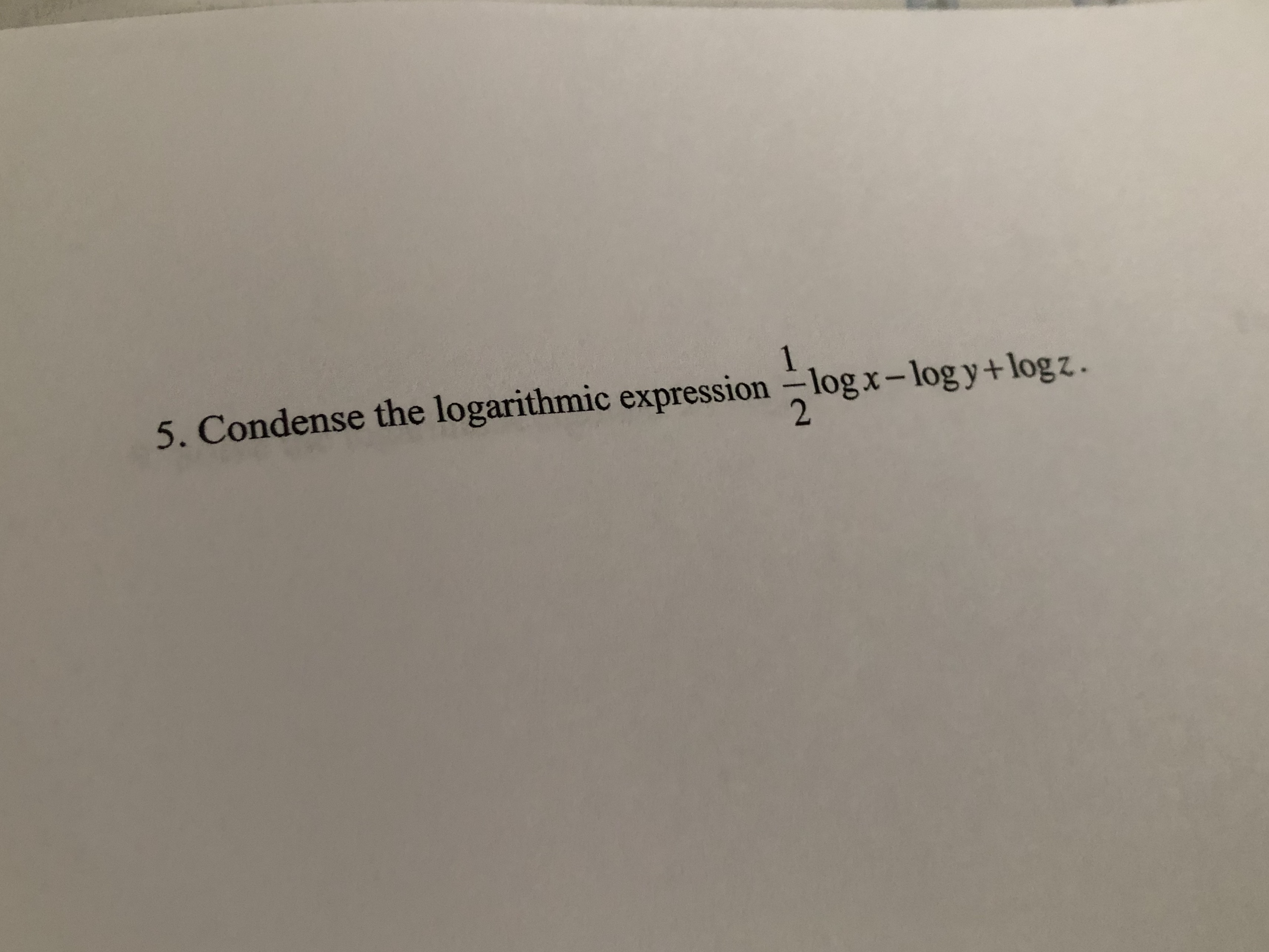

We can represent this statement symbolically as To start with, the logarithm of a number ‘b’ can be defined as the power or exponent to which another number ‘a’ must be raised to produce the result equal to the number b. What is a logarithm? Why do we study them? And what are their rules and laws?


 0 kommentar(er)
0 kommentar(er)
